2025-3S 計算数理演習（東京大学理学部・教養学部） [齊藤宣一] [top] [0] [1] [2] [3] [4] [5] [6] [7] [8] [UTOL]

5. 固有値問題

$A\in\mathbb{C}^{n\times n}$（$=n\times n$ 複素行列全体の集合）に対する固有値問題 \[ \lambda\in\mathbb{C},\quad \boldsymbol{0}\ne\boldsymbol{v}\in\mathbb{C}^{n},\quad A\boldsymbol{v}=\lambda\boldsymbol{v} \] を考察する．

例5.1

例題として， $\displaystyle{ A=\begin{pmatrix} 5 & 4 & 1 & 1\\ 4 & 5 & 1 & 1\\ 1 & 1 & 4 & 2\\ 1 & 1 & 2 & 4 \end{pmatrix}}$ を考える．絶対値最大の固有値は $\lambda=10$，（正規化された）固有ベクトルは， $\displaystyle{\boldsymbol{v} =\begin{pmatrix} 2/\sqrt{10}\\ 2/\sqrt{10}\\ 1/\sqrt{10}\\ 1/\sqrt{10} \end{pmatrix} \approx \begin{pmatrix} 0.6325\\ 0.6325\\ 0.3162\\ 0.3162 \end{pmatrix} }$ となる．答えがわかっているのだから，近似計算をする必要はないが，近似解法の妥当性を確認するために，あえて，答えのわかっている問題で試すのである．$\blacksquare$

固有値と固有ベクトルを求めることは， numpyの linalgを用いれば容易い．

In [1]:  
import numpy as np
import matplotlib.pyplot as plt
from numpy import linalg as la

In [2]:  
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])

eval, evect = np.linalg.eig(A)
print("eigenvalues\n",eval)
print("eigenvectors\n",evect)
print("eigenvalue\n",eval[0])
print("eigenvector\n",evect[:,0])
  
Out [3]:
eigenvalues
 [10.  1.  5.  2.]
eigenvectors
 [[-6.32455532e-01 -7.07106781e-01  3.16227766e-01  1.66533454e-16]
 [-6.32455532e-01  7.07106781e-01  3.16227766e-01 -6.74454005e-17]
 [-3.16227766e-01 -5.94276718e-17 -6.32455532e-01 -7.07106781e-01]
 [-3.16227766e-01 -8.70027738e-17 -6.32455532e-01  7.07106781e-01]]
eigenvalue
 9.999999999999996
eigenvector
 [-0.63245553 -0.63245553 -0.31622777 -0.31622777]

関数eig をブラックボックス的に使うのであれば，それ以上考察することはない．しかし，本節では，「具体的にどのようなアルゴリズムで固有値を計算することができるのか」および「その数学的妥当性」を検討する．

固有値を求めるには，最も素朴には，固有多項式を構成して，Newton法を適用することが考えられる．しかし，$n$ が大きい時には，実用的でない．

本節では，固有値（実は固有ベクトル）の代表的な近似計算方法である冪乗法と逆冪乗法を紹介する．これらは，特定の固有値を求める方法である．一方で，すべての固有値を同時に求める方法もある．QR法はその代表である．実は，関数eigでは，QR法に基づいた方法で計算を行っている．QR法については，本節の最後に付録として簡単に紹介する．

以下では，次の記号を用いる．

$\mathbb{C}^n$の内積 $\displaystyle{\langle\boldsymbol{x},\boldsymbol{y}\rangle=\sum_{i=1}^nx_i\overline{y_i}} \quad (\boldsymbol{x}=(x_i),~\boldsymbol{y}=(y_i)\in\mathbb{C}^n)$
$\mathbb{C}^n$ のノルム $\displaystyle{\|\boldsymbol{x}\|= \left(\sum_{i=1}^n|x_i|^2 \right)^{1/2}}$
Rayleigh商 $\displaystyle{R_A(\boldsymbol{x})= \frac{\langle A\boldsymbol{x},\boldsymbol{x}\rangle}{~\|\boldsymbol{x}\|^2}\in\mathbb{C}} \quad (\boldsymbol{x}\ne \boldsymbol{0})$

このとき，次が成り立つことに注意せよ．

$\|\boldsymbol{x}\|^2=\langle\boldsymbol{x},\boldsymbol{x}\rangle$
Cauchy--Schwarzの不等式 $|\langle\boldsymbol{x},\boldsymbol{y}\rangle|\le \|\boldsymbol{x}\|\|\boldsymbol{y}\|$
$A\boldsymbol{v}=\lambda\boldsymbol{v}$，$\boldsymbol{v}\ne\boldsymbol{0}$ ならば，$R_A(\boldsymbol{v})=\lambda$．（固有ベクトルが得られれば，Rayleigh商により固有値が算出できる．）
任意の $0\ne \alpha\in\mathbb{C}$ に対して， $R_A(\alpha\boldsymbol{x})=R_A(\boldsymbol{x})$．
$A$ がエルミートならば，$R_A(\boldsymbol{x})\in\mathbb{R}$．

冪乗法

$A$ の固有値を$\lambda_1,\ldots,\lambda_n\in\mathbb{C}$，対応する固有ベクトルを $\boldsymbol{v}_1,\ldots,\boldsymbol {v}_n$ とする．さらに，$|\lambda_1|\le|\lambda_2|\le\cdots \le |\lambda_n|$ と並べておく．

そして，暫くの間（冪乗法と逆冪乗法の説明の間は）$A$ に対して，次を仮定する： \begin{equation} \tag{$\star$} |\lambda_1| \le \cdots \le |\lambda_{n-1}|<|\lambda_n| \quad \mbox{かつ}\quad A\mbox{ は対角化可能}. \end{equation} そして，絶対値が最大の固有値 $\lambda_n$ を求める．

$\boldsymbol{x}\in\mathbb{C}^n$ を任意とし， $\boldsymbol{x}=c_1\boldsymbol{v}_1+\cdots+c_n\boldsymbol{v}_n$ と書く（「$A$は対角化可能 $\Leftrightarrow$ $\boldsymbol{v}_1,\ldots,\boldsymbol{v}_n$ は一次独立」に注意せよ）．$1\le k\in \mathbb{Z}$ に対して， \begin{align*} \boldsymbol{x}' &\stackrel{\textrm{def.}}{=} A^k\boldsymbol{x}\\ &= c_1\lambda_1^k\boldsymbol{v}_1+\cdots+c_n\lambda_n^k\boldsymbol{v}_n \nonumber \\ &= c_n\lambda_n^k \left[\frac{c_1}{c_n}\left(\frac{\lambda_1}{\lambda_n}\right)^k\boldsymbol{v}_1+\cdots+\frac{c_{n-1}}{c_n} \left(\frac{\lambda_{n-1}}{\lambda_n}\right)^k\boldsymbol{v}_{n-1}+\boldsymbol{v}_n\right] \end{align*} となるので，$c_n\ne 0$ かつ $k$ が十分大きければ， \[ \boldsymbol{x}'\approx \lambda_n^kc_n\boldsymbol{v}_n \] が期待できる．そして， $R_A(\lambda_n^kc_n\boldsymbol{v}_n)=R_A(\boldsymbol{v}_n)=\lambda_n$ なので，この関係により，近似固有値 $\tilde{\lambda}=R_A(\boldsymbol{x}')$ を得ることができる．

冪乗法のアルゴリズム

$\boldsymbol{x}^{(0)}\in\mathbb{C}^n$ を初期値として，次のように点列 $\boldsymbol{x}^{(k)}$ ($k=1,2,\ldots$) を生成する： \[ \boldsymbol{y}^{(k)}=A\boldsymbol{x}^{(k)},\quad \boldsymbol{x}^{(k+1)}=\frac{1}{\|\boldsymbol{y}^{(k)}\|}\boldsymbol{y}^{(k)}. \] このとき，近似固有値は $\mu^{(k)}=R_A(\boldsymbol{x}^{(k)})$ で与えられる．$\blacksquare$

注意. 単純に，$\boldsymbol{x}^{(k+1)}=A\boldsymbol{x}^{(k)}$ とすると，ほとんどの場合，$\|\boldsymbol{x}^{(k)}\|\to\infty$ あるいは $\|\boldsymbol{x}^{(k)}\|\to 0$ となる．一方で，必要なのは $\boldsymbol{x}^{(k)}$ の向きに関する情報のみである．

注意. 明らかに，$\|\boldsymbol{x}^{(k)}\|=1$ $(k\ge 1)$ となる．

冪乗法のプログラムの例をIn [3]に示す．

In [3]:
def power1(A, initial, tolerance):
  kmax = 100
  eval = np.array([])
  increment = np.array([])
  evec = np.copy(init)
  k = 0
  x = initial / la.norm(initial, ord=2)
  muold = 0
  inc = tolerance + 1
  while k <= kmax and inc >= tolerance:
    y = A@x
    mu = np.vdot(y, x)
    inc = np.abs((mu - muold) / mu)
    eval = np.append(eval, mu)
    increment = np.append(increment, inc)
    evec = np.vstack((evec, x))
    x = y / la.norm(y, ord=2)
    muold = mu
    k += 1
  return k, eval, increment, evec[1:,:]

まずは，ともかく実行してみよう．

In [4]:  
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
init = np.array([1, 0, 0, 0])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = power1(A, init, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
  
Out [4]: 
反復, 固有値, 増分, 固有ベクトル
0, 5.0000, 1.000e+00,  [1. 0. 0. 0.]
1, 9.6047, 4.794e-01,  [0.76249285 0.60999428 0.15249857 0.15249857]
2, 9.9220, 3.198e-02,  [0.67459799 0.65890967 0.23532488 0.23532488]
3, 9.9805, 5.867e-03,  [0.65173824 0.65016019 0.27616027 0.27616027]
4, 9.9951, 1.460e-03,  [0.64210325 0.64194522 0.29631888 0.29631888]
5, 9.9988, 3.658e-04,  [0.6373267  0.63731089 0.30630826 0.30630826]
6, 9.9997, 9.153e-05,  [0.63490748 0.6349059  0.31127721 0.31127721]
7, 9.9999, 2.289e-05,  [0.63368604 0.63368588 0.31375484 0.31375484]
8, 10.0000, 5.722e-06,  [0.63307196 0.63307195 0.3149919  0.3149919 ]
9, 10.0000, 1.431e-06,  [0.63276405 0.63276405 0.31560998 0.31560998]
10, 10.0000, 3.576e-07,  [0.63260986 0.63260986 0.31591891 0.31591891]
11, 10.0000, 8.941e-08,  [0.63253272 0.63253272 0.31607335 0.31607335]
12, 10.0000, 2.235e-08,  [0.63249413 0.63249413 0.31615056 0.31615056]
13, 10.0000, 5.588e-09,  [0.63247483 0.63247483 0.31618916 0.31618916]

確かに，絶対値最大の固有値とその固有ベクトルが，かなり正確に求められている．

このプログラムでは，与えられたtoleranceに対して， \[ \mbox{inc}=\mbox{inc}_k\stackrel{\textrm{def.}}{=} \left| \frac{\mu_{k}-\mu_{k-1}}{\mu_{k}}\right|\le \mbox{tolerance} \] が満たされた時点で，これ以上反復を続けても数値が改善されないと判断して，計算を終了する．

技術的な注意を述べる．eval，increment，evec は， \[ \mbox{eval} =\begin{pmatrix} \mu_0\\ \mu_1\\ \vdots\\ \mu_m \end{pmatrix} ,\quad \mbox{increment} =\begin{pmatrix} \mbox{inc}_0\\ \mbox{inc}_1\\ \vdots\\ \mbox{inc}_m \end{pmatrix} ,\quad \mbox{evec} =\begin{pmatrix} \boldsymbol{x}_0^{\scriptsize \mbox{T}}\\ \boldsymbol{x}_1^{\scriptsize \mbox{T}}\\ \vdots\\ \boldsymbol{x}_m^{\scriptsize \mbox{T}} \end{pmatrix} \] である．ただし， $\mbox{inc}_{0}=1$ としており， $\mbox{inc}_{k+1}<\mbox{tolerance}$ を満たす最小の $k$ を $m$ と書いている． $\boldsymbol{x}_k^{\scriptsize \mbox{T}}$ は $\boldsymbol{x}_k$ の転置である．

これらを生成するため，最初に eval = np.array([]) により，空の配列としてeval を定義して，np.appendにより，最後尾に順に $\mu_0,\mu_1,\ldots$ を追加している． evecについても，np.vstackにより，最後尾（最終行）に順に $\boldsymbol{x}_0,\boldsymbol{x}_1,\ldots$ を追加している．ただし，np.vstack を利用する際には，対象となる配列の列数はすでに決定されていなければならない．そのため， evecを定義する際には， evec = np.copy(init)としている．しかし，このようにすると，最初の行（第0行）と次の行（第1行）に $\boldsymbol{x}_0$ が格納されることになる．したがって，計算結果を返す際に，evec[1:,:] として，第1行以降のみを返すようにしているのである．（もっと上手いやり方のわかる人は，ぜひ教えてください．）

In [5]:  
x = np.array([])
print(x.shape)
print(x)
x=np.append(x,2.0)
print(x.shape)
print(x)
x=np.append(x,4.0)
print(x.shape)
print(x)

y = np.array([[0, 0]])
y = np.vstack((y,[1,2]))
print(y.shape)
print(y)
y=np.vstack((y,[3,4]))
print(y.shape)
print(y)
  
Out [5]: 
(0,)
[]
(1,)
[2.]
(2,)
[2. 4.]
(2, 2)
[[0 0]
 [1 2]]
(3, 2)
[[0 0]
 [1 2]
 [3 4]]

もう一つ，np.vdot(y,x)$\displaystyle{=\sum_{i=1}^n x_i\overline{y_i}}$ であることに注意せよ．

In [6]:  
x=np.array([1+2j,2-1j])
y=np.array([3-1j,4+5j])
print(np.vdot(x,y))
print(np.vdot(y,x))
  
Out [6]: 
(4+7j)
(4-7j)

さて，改めて，初期ベクトルをかえて，冪乗法を実行してみよう．

In [7]:  
init = np.array([1, 1, 1, 1])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = power1(A, init, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
  
Out [7]: 
反復, 固有値, 増分, 固有ベクトル
0, 9.5000, 1.000e+00,  [0.5 0.5 0.5 0.5]
1, 9.8649, 3.699e-02,  [0.5719 0.5719 0.4159 0.4159]
2, 9.9655, 1.010e-02,  [0.604  0.604  0.3677 0.3677]
3, 9.9913, 2.584e-03,  [0.6187 0.6187 0.3423 0.3423]
4, 9.9978, 6.498e-04,  [0.6257 0.6257 0.3293 0.3293]
5, 9.9995, 1.627e-04,  [0.6291 0.6291 0.3228 0.3228]
6, 9.9999, 4.069e-05,  [0.6308 0.6308 0.3195 0.3195]
7, 10.0000, 1.017e-05,  [0.6316 0.6316 0.3179 0.3179]
8, 10.0000, 2.543e-06,  [0.632  0.632  0.3171 0.3171]
9, 10.0000, 6.358e-07,  [0.6322 0.6322 0.3166 0.3166]
10, 10.0000, 1.589e-07,  [0.6324 0.6324 0.3164 0.3164]
11, 10.0000, 3.974e-08,  [0.6324 0.6324 0.3163 0.3163]
12, 10.0000, 9.934e-09,  [0.6324 0.6324 0.3163 0.3163]

In [8]:  
init = np.array([2, 2, 1, 1])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = power1(A, init, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])

Out [8]: 

反復, 固有値, 増分, 固有ベクトル
0, 10.0000, 1.000e+00,  [0.6325 0.6325 0.3162 0.3162]
1, 10.0000, 0.000e+00,  [0.6325 0.6325 0.3162 0.3162]

ここまでは，順調である．しかし，次はどうであろうか？

In [9]:  
init = np.array([1, 2, 3, -9])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = power1(A, init, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
  
Out [9]: 
反復, 固有値, 増分, 固有ベクトル
0, 2.7053, 1.000e+00,  [ 0.1026  0.2052  0.3078 -0.9234]
1, 3.9824, 3.207e-01,  [ 0.24    0.2742 -0.1028 -0.9255]
2, 4.7727, 1.656e-01,  [ 0.3     0.3081 -0.4135 -0.8026]
3, 4.9612, 3.799e-02,  [ 0.3133  0.315  -0.5479 -0.7088]
4, 4.9937, 6.516e-03,  [ 0.3157  0.3161 -0.5994 -0.6641]
5, 4.9990, 1.055e-03,  [ 0.3161  0.3162 -0.6194 -0.6453]
6, 4.9998, 1.691e-04,  [ 0.3162  0.3162 -0.6273 -0.6376]
7, 5.0000, 2.706e-05,  [ 0.3162  0.3162 -0.6304 -0.6345]
8, 5.0000, 4.329e-06,  [ 0.3162  0.3162 -0.6316 -0.6333]
9, 5.0000, 6.927e-07,  [ 0.3162  0.3162 -0.6321 -0.6328]
10, 5.0000, 1.108e-07,  [ 0.3162  0.3162 -0.6323 -0.6326]
11, 5.0000, 1.773e-08,  [ 0.3162  0.3162 -0.6324 -0.6325]
12, 5.0000, 2.837e-09,  [ 0.3162  0.3162 -0.6324 -0.6325]

この場合，絶対値最大の固有値が求められていない．（しかし，$5$ 自体は $A$ の固有値である．）一方で，初期ベクトルを少しだけずらすと，以下のように反復回数は多くなるものの，絶対値最大の固有値が求められる．

In [10]:  
init = np.array([1.1, 2, 3, -9])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = power1(A, init, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
  
Out [10]: 
反復, 固有値, 増分, 固有ベクトル
0, 2.7145, 1.000e+00,  [ 0.1127  0.205   0.3075 -0.9224]
1, 3.9944, 3.204e-01,  [ 0.2559  0.2866 -0.099  -0.9179]
2, 4.7891, 1.659e-01,  [ 0.3323  0.3396 -0.3983 -0.7846]
3, 5.0169, 4.542e-02,  [ 0.378   0.3794 -0.5124 -0.6713]
4, 5.2085, 3.679e-02,  [ 0.4399  0.4402 -0.5212 -0.584 ]
5, 5.7604, 9.580e-02,  [ 0.5379  0.5379 -0.447  -0.4707]
6, 7.0904, 1.876e-01,  [ 0.6502  0.6502 -0.274  -0.2819]
7, 8.7094, 1.859e-01,  [ 0.7054  0.7054 -0.0479 -0.05  ]
8, 9.5999, 9.276e-02,  [0.6961 0.6961 0.1246 0.1242]
9, 9.8936, 2.968e-02,  [0.6718 0.6718 0.2206 0.2205]
10, 9.9730, 7.959e-03,  [0.654  0.654  0.2689 0.2689]
11, 9.9932, 2.026e-03,  [0.6437 0.6437 0.2927 0.2927]
12, 9.9983, 5.089e-04,  [0.6382 0.6382 0.3045 0.3045]
13, 9.9996, 1.274e-04,  [0.6353 0.6353 0.3104 0.3104]
14, 9.9999, 3.185e-05,  [0.6339 0.6339 0.3133 0.3133]
15, 10.0000, 7.963e-06,  [0.6332 0.6332 0.3148 0.3148]
16, 10.0000, 1.991e-06,  [0.6328 0.6328 0.3155 0.3155]
17, 10.0000, 4.977e-07,  [0.6326 0.6326 0.3159 0.3159]
18, 10.0000, 1.244e-07,  [0.6325 0.6325 0.316  0.316 ]
19, 10.0000, 3.111e-08,  [0.6325 0.6325 0.3161 0.3161]
20, 10.0000, 7.777e-09,  [0.6325 0.6325 0.3162 0.3162]

これらの現象を説明するために，冪乗法の収束に関して，次の結果を復習しよう．例えば，[齊藤2012]の定理5.2.1を見よ．

定理 5.1. $(\star)$を仮定し，さらに，$\|\boldsymbol{x}^{(0)}\|=1$ かつ $\boldsymbol{x}^{(0)}\not\in\mbox{span}~\{\boldsymbol{v}_1,\ldots,\boldsymbol{v}_{n-1}\}$ とする．このとき，$r=|\lambda_{n-1}/\lambda_n|(<1)$ とおくと， \begin{equation*} |\lambda_n-\mu^{(k)}|\le Cr^k\qquad (k\ge k_0) \end{equation*} を満たす定数 $C>0$ と $0 < k_0 \in\mathbb{Z}$ が存在する．また， \begin{equation*} \left\|\frac{\|A^k\boldsymbol{x}^{(0)}\|}{c_n\lambda_n^k}\boldsymbol{x}^{(k)}-\boldsymbol{v}_n\right\| \le C' r^k\qquad (k\ge k_0) \end{equation*} を満たす定数 $C ' >0$ が存在する．$\blacksquare$

あらためて，In [9]では，初期ベクトルを $\boldsymbol{x}^{(0)}=(1,2,3,-9)^{\scriptsize \mbox{T}}$ と選ぶと，近似固有値として $\lambda_3=5$ が得られている．これは，$\langle \boldsymbol{v}_4,\boldsymbol{x}^{(0)}\rangle=0$，すなわち， $\boldsymbol{x}^{(0)}\in\operatorname{span}\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\}$ となっており，定理の仮定が満たされていないためであり，定理とは矛盾しない．実際，In [10]では，$\boldsymbol{x}^{(0)}$ を少しだけずらして，$\boldsymbol{x}^{(0)}=(1.1,2,3,-9)^{\scriptsize \mbox{T}}$ とすることで，正しく $\lambda_4=10$ が得られている．

逆冪乗法

まず， \[ A\boldsymbol{v}_1=\lambda_1\boldsymbol{v}_1\quad\Leftrightarrow\quad A^{-1}\boldsymbol{v}_1=\lambda_1^{-1}\boldsymbol{v}_1 \] なので，$\lambda_1^{-1}$ は，$A^{-1}$ の絶対値最大の固有値となる．したがって，絶対値最小の固有値が唯一存在するならば，すなわち， $|\lambda_1|< |\lambda_i|$（$i\ge 2$）ならば， $A^{-1}$ に冪乗法を適用することにより，$1/\lambda_1$ が得られる．

次に，$\alpha\in\mathbb{C}$ に対して， $B=A-\alpha I$ の固有値は $\mu_i=\lambda_i-\alpha$，対応する固有ベクトルは $\boldsymbol{v}_i$ となる．ここで， \begin{equation*} |\mu_k|<|\mu_i| \quad\Leftrightarrow\quad |\lambda_k-\alpha|<|\lambda_i-\alpha| \quad (i\ne k) \end{equation*} を満たす $\lambda_k$ の存在を仮定する．すなわち，$\lambda_k$ は $\alpha$ に最も近い $A$ の固有値である．このとき，$E=B^{-1}=(A-\alpha I)^{-1}$ とおくと， \[ \lambda_k=R_A(\boldsymbol{v}_k),\quad \mu_k=R_B(\boldsymbol{v}_k), \quad \mu_k^{-1}=R_E(\boldsymbol{v}_k) \] が成り立つことに注意せよ． $E$ に冪乗法を適用することで，$\boldsymbol{v}_k$ の近似値が得られるので， $\mu_k$ や $\lambda_k$ の近似値が計算できる．

逆冪乗法（逆反復法）のアルゴリズム

$\alpha\in\mathbb{C}$ の最も近くにある固有値 $\lambda$ を計算するために，反復列を次で生成する： \begin{equation*} \boldsymbol{y}^{(k)}=(A-\alpha I)^{-1}\boldsymbol{x}^{(k)},\quad \boldsymbol{x}^{(k+1)}=\frac{1}{\|\boldsymbol{y}^{(k)}\|}\boldsymbol{y}^{(k)} \quad (k=0,1,\ldots). \end{equation*} なお，$\boldsymbol{y}^{(k)}$は，連立一次方程式 \begin{equation*} (A-\alpha I)\boldsymbol{y}^{(k)}=\boldsymbol{x}^{(k)} \end{equation*} を解いて求める．このとき，$\boldsymbol{x}^{(k+1)}$ が近似固有ベクトルである．近似固有値 $\tilde{\lambda}$ は，次で得られる： \[ \tilde{\lambda}=R_A(\boldsymbol{x}^{(k+1)})=\frac{1}{R_E(\boldsymbol{x}^{(k+1)})}+\alpha. \] ただし，$E=(A-\alpha I)^{-1}$ とおいている．$\blacksquare$

In [11]:
def invpower1(A, initial, alpha, tolerance):
  kmax = 100
  eval = np.array([])
  increment = np.array([])
  evec = np.copy(init)
  E = A - alpha * np.eye(A.shape[0])
  k = 0
  x = init / la.norm(init, ord=2)
  muold = 0
  inc = tolerance + 1
  while k <= kmax and inc >= tolerance:
    y = la.solve(E, x)
    mu = np.vdot(x, y)
    inc = np.abs((mu - muold) / mu)
    eval = np.append(eval, 1/mu + alpha)
    increment = np.append(increment, inc)
    evec = np.vstack((evec, x))
    x = y / la.norm(y, ord=2)
    muold = mu
    k += 1
  return k, eval, increment, evec[1:, :]

まずは，絶対値最小の固有値を求めてみよう．

In [12]:  
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
init = np.array([1, 0, 0, 0])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = invpower1(A, init, 0, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
  
Out [12]: 
反復, 固有値, 増分, 固有ベクトル
0, 1.7857, 1.000e+00,  [1. 0. 0. 0.]
1, 1.0136, 4.324e-01,  [ 0.78569895 -0.61733489 -0.02806068 -0.02806068]
2, 1.0003, 1.306e-02,  [ 0.71827685 -0.69565396 -0.00848358 -0.00848358]
3, 1.0000, 3.169e-04,  [ 0.70879902 -0.70540493 -0.00197989 -0.00197989]
4, 1.0000, 1.054e-05,  [ 7.07389440e-01 -7.06823755e-01 -4.24263958e-04 -4.24263958e-04]
5, 1.0000, 4.003e-07,  [ 7.07157686e-01 -7.07055862e-01 -8.76812400e-05 -8.76812400e-05]
6, 1.0000, 1.580e-08,  [ 7.07116398e-01 -7.07097164e-01 -1.78190909e-05 -1.78190909e-05]
7, 1.0000, 6.299e-10,  [ 7.07108648e-01 -7.07104914e-01 -3.59210245e-06 -3.59210245e-06]

$\alpha$ を変化させると，いろいろな固有値が求められる．ただし，初期ベクトルの取り方次第では，予期せぬ固有値を求めることがある．

In [13]:  
init = np.array([1, 2, 3, 4])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = invpower1(A, init, 3.0, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
  
Out [13]: 
反復, 固有値, 増分, 固有ベクトル
0, 6.8889, 1.000e+00,  [0.18257419 0.36514837 0.54772256 0.73029674]
1, 6.9978, 2.801e-02,  [ 0.03573708 -0.21442251  0.89342711  0.39310793]
2, -6.4842, 3.372e+00,  [-0.3049266  -0.08520008  0.06726322  0.94616931]
3, 1.2973, 8.205e-01,  [-0.08075426 -0.23047701  0.93282079 -0.26496126]
4, 1.8494, 3.243e-01,  [-0.13347429 -0.04913961 -0.48841052  0.86094429]
5, 1.9637, 9.928e-02,  [-0.02597999 -0.06964021  0.79472391 -0.60240285]
6, 1.9910, 2.638e-02,  [-0.03521592 -0.0131865  -0.65646127  0.7534219 ]
7, 1.9978, 6.702e-03,  [-0.00661957 -0.01765963  0.73085397 -0.68227326]
8, 1.9994, 1.682e-03,  [-0.0088365  -0.00331329 -0.69481949  0.71912225]
9, 1.9999, 4.210e-04,  [-0.00165711 -0.00441911  0.71314925 -0.70099634]
10, 2.0000, 1.053e-04,  [-0.00220967 -0.00082862 -0.70405997  0.7101366 ]
11, 2.0000, 2.632e-05,  [-4.14317275e-04 -1.10484917e-03  7.08623828e-01 -7.05585486e-01]
12, 2.0000, 6.580e-06,  [-5.52426492e-04 -2.07159769e-04 -7.06346663e-01  7.07865837e-01]
13, 2.0000, 1.645e-06,  [-1.03580038e-04 -2.76213497e-04  7.07486442e-01 -7.06726855e-01]
14, 2.0000, 4.113e-07,  [-1.38106781e-04 -5.17900396e-05 -7.06916851e-01  7.07296645e-01]
15, 2.0000, 1.028e-07,  [-2.58950226e-05 -6.90533950e-05  7.07201721e-01 -7.07011824e-01]
16, 2.0000, 2.570e-08,  [-3.45266981e-05 -1.29475117e-05 -7.07059305e-01  7.07154253e-01]
17, 2.0000, 6.426e-09,  [-6.47375591e-06 -1.72633491e-05  7.07130518e-01 -7.07083044e-01]

In [14]:  
init = np.array([1, 0, 1, 1])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = invpower1(A, init, 2.1, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])
  
Out [14]:
反復, 固有値, 増分, 固有ベクトル
0, 53.5306, 1.000e+00,  [0.57735027 0.         0.57735027 0.57735027]
1, 0.4730, 1.032e+00,  [-0.61817401  0.61226618  0.34856206  0.34856206]
2, 0.9411, 2.877e-01,  [ 0.65551242 -0.73226355  0.13056331  0.13056331]
3, 0.9918, 4.375e-02,  [-0.72525638  0.68516524  0.04770625  0.04770625]
4, 0.9988, 6.324e-03,  [ 0.69848014 -0.71518802  0.01777065  0.01777065]
5, 0.9998, 9.107e-04,  [-0.71033942  0.70379567  0.00669177  0.00669177]
6, 1.0000, 1.310e-04,  [ 0.70584581 -0.70835647  0.00253127  0.00253127]
7, 1.0000, 1.885e-05,  [-0.70758411  0.70662783  0.00095915  0.00095915]
8, 1.0000, 2.713e-06,  [ 7.06925024e-01 -7.07288304e-01  3.63681013e-04  3.63678508e-04]
9, 1.0000, 3.903e-07,  [-7.07175701e-01  7.07037828e-01  1.37914549e-04  1.37942104e-04]
10, 1.0000, 5.615e-08,  [ 7.07080625e-01 -7.07132932e-01  5.24665250e-05  5.21634158e-05]
11, 1.0000, 8.134e-09,  [-7.07116702e-01  7.07096860e-01  1.81761365e-05  2.15103385e-05]

In [15]: 
init = np.array([1, 0, 0, 0])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = invpower1(A, init, 5.7, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:]) 
  
Out [15]: 
反復, 固有値, 増分, 固有ベクトル
0, -0.7014, 1.000e+00,  [1. 0. 0. 0.]
1, 4.8475, 8.668e-01,  [-0.31347013  0.11347335  0.66665594  0.66665594]
2, 4.9962, 1.745e-01,  [ 0.38381183  0.31385033 -0.61407917 -0.61407917]
3, 4.9999, 5.200e-03,  [-0.31597406 -0.30552752  0.63514303  0.63514303]
4, 5.0000, 1.297e-04,  [ 0.31789358  0.31633762 -0.63201036 -0.63201036]
5, 5.0000, 3.241e-06,  [-0.31619901 -0.31596727  0.63252781  0.63252781]
6, 5.0000, 8.153e-08,  [ 0.31626856  0.31623405 -0.63244376 -0.63244376]
7, 5.0000, 2.064e-09,  [-0.3162265  -0.31622136  0.63245745  0.63245745]

Gershgorinの定理

逆冪乗法を利用するにあたり，固有値の存在範囲についての情報があると便利である． $A=(a_{i,j})\in\mathbb{C}^{n\times n}$ の固有値 $\lambda_1,\ldots,\lambda_n$ について， $\displaystyle{\rho(A)=\max_{1\le i\le n}|\lambda_i|}$ を $A$ のスペクトル半径と呼ぶ．

定理 5.2. $\displaystyle{\rho(A)\le \max_{1\le i\le n}\sum_{j=1}^n|a_{i,j}|}$ である．$\blacksquare$

これで固有値の大雑把な存在範囲として，複素平面上の原点中心，半径 $\displaystyle{\max_{1\le i\le n}\sum_{j=1}^n|a_{i,j}|}$ の円盤を取れることがわかる．定理 5.2の証明は簡単である． $\lambda\in\mathbb{C}$ と $\boldsymbol{v}=(v_1,\ldots,v_n)^{\scriptsize \mbox{T}}\ne\boldsymbol{0}$ を， $|\lambda|=\rho(A)$，$A\boldsymbol{v}=\lambda\boldsymbol{v}$ を満たすものとして，$\displaystyle{|v_k|=\max_{1\le i\le n}|v_i|}$ とおく．$A\boldsymbol{v}=\lambda\boldsymbol{v}$ の第 $k$ 成分は， $\displaystyle{\lambda v_k=\sum_{j=1}^na_{k,j}v_j}$　であり，したがって， $\displaystyle{|\lambda| \le \sum_{j=1}^n|a_{k,j}|\frac{|v_j|}{|v_k|}\le \sum_{j=1}^n|a_{k,j}|}$ が得られ，これより所望の不等式が従う．この証明とほぼ同様の考察をすることで，より精密な固有値の存在範囲を求める次の定理（例えば，[齊藤2012]の定理5.1.1）が証明できる．

定理 5.3.（Gershgorin） $A=(a_{i,j})\in\mathbb{C}^{n\times n}$ のすべての固有値は $\displaystyle{G=\bigcup_{i=1}^nG_{i}}$ の中に含まれる．ただし，$G_i =\{z\in\mathbb{C}\mid |z-a_{i,i}|\le r_i\}$，かつ， $\displaystyle{r_i=\sum_{1\le j\le n,j\ne i}|a_{i,j}|}$ である．$\blacksquare$

各 $G_i$ のことをGershgorinの円盤と呼ぶ．

In [16]:
def gershgorin(A):
    A = np.array(A)
    n = len(A)
    centers = np.diag(A)
    radii = np.sum(np.abs(A - np.diag(centers)), axis=1)
    bounds = np.array([
        centers.real - radii,
        centers.real + radii,
        centers.imag - radii,
        centers.imag + radii])

    fig, ax = plt.subplots()
    for center, radius in zip(centers, radii):
        circle = plt.Circle((center.real, center.imag), radius, color='b', fill=False)
        ax.add_artist(circle)

    print(f"実部の範囲: {bounds[0].min():.2f}, {bounds[1].max():.2f}")
    print(f"虚部の範囲: {bounds[2].min():.2f}, {bounds[3].max():.2f}")

    plt.xlim(bounds[0].min(), bounds[1].max())
    plt.ylim(bounds[2].min(), bounds[3].max())
    ax.set_aspect('equal')
    ax.set_xlabel('Real')
    ax.set_ylabel('Imaginary')
    ax.grid(True)
    plt.show()

In [17]:  
A = np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
gershgorin(A)
  
Out [17]: 
実部の範囲: -1.00, 11.00
虚部の範囲: -6.00, 6.00

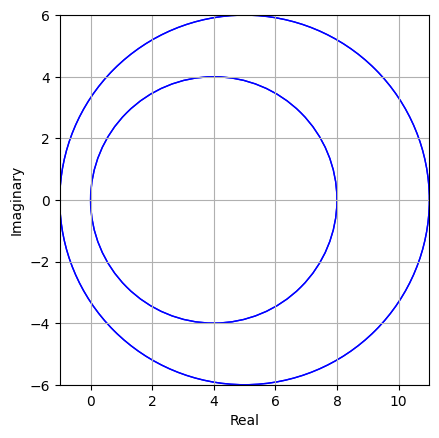
$A$ についてGershgorinの円盤を計算してみると，Out [17]と図5.1のようになる．これより，絶対値最大の固有値について $|\lambda_4|\le 11$ という評価が得られるので（この情報を得るだけなら，定理5.2を使ったほうが早い），この情報を利用して，$\alpha=11$ と選んで，逆冪乗法を適用するとOut [18]のようになる．

Out [4] と比較すると，単純に冪乗法を適用するよりも，少ない反復回数で，近似固有値が得られていることがわかる．ただし，冪乗法では一回の反復で行列とベクトルの積を計算するのみであるが，逆冪乗法では連立一次方程式を計算しなければならないので，反復回数のみでは，計算の手間の比較はできない．

In [18]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
init = np.array([1, 0, 0, 0])  # 初期ベクトル
tol = 1e-8  # 許容誤差

iteration, eval, increment, evec = invpower1(A, init, 11, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])   
  
Out [18]: 
反復, 固有値, 増分, 固有ベクトル
0, 8.8571, 1.000e+00,  [1. 0. 0. 0.]
1, 9.9830, 5.254e-01,  [-0.73079405 -0.57419533 -0.26099788 -0.26099788]
2, 9.9997, 1.644e-02,  [0.64465082 0.62884194 0.3073948  0.3073948 ]
3, 10.0000, 2.676e-04,  [-0.63397602 -0.63239488 -0.31476271 -0.31476271]
4, 10.0000, 5.455e-06,  [0.63265654 0.63249843 0.31598374 0.31598374]
5, 10.0000, 1.317e-07,  [-0.63248377 -0.63246796 -0.3161871  -0.3161871 ]
6, 10.0000, 3.461e-09,  [0.63245971 0.63245813 0.31622099 0.31622099]

GoogleのPageRank

GoogleのPageRankは，1998年にSergey BrinとLawrence Pageによって開発されたアルゴリズムで，大雑把には「多くの重要なページからリンクされているページは重要である」という考えに基づいて，ウェブページの重要度を数値で評価するものである（[BP1998]，[PBMW1999]）．もちろん，現在では，PageRankのみでウェブページの重要度を評価しているわけではないが，現在でも複雑なアルゴリズムの一要素として現役である（そのようです）．

$N$ 個のウェブページ $W_1,\ldots,W_N$ があるとする．PageRankにおける最も基本的な考え方は，各ウェブの重要度を表現する量 $p_1,\ldots,p_N$ を， \begin{gather} p_i \ge 0 \quad (i=1,\ldots,N),\tag{5.1}\\ p_1+\cdots+p_N= 1,\tag{5.2} \\ p_i=\sum_{j\in B_i}\frac{p_j}{|W_j|}\quad (i=1,\ldots,N)\tag{5.3} \end{gather} により定めることである．ただし，$B_i$ は $W_i$ にリンクが張られているウェブページの番号の集合，すなわち，$B_i=\{ j \mid W_j \mbox{ から } W_i \mbox{ へのリンクが張られている}\}$ であり， $|W_j|$ は $W_j$ が張っているリンクの総数である．

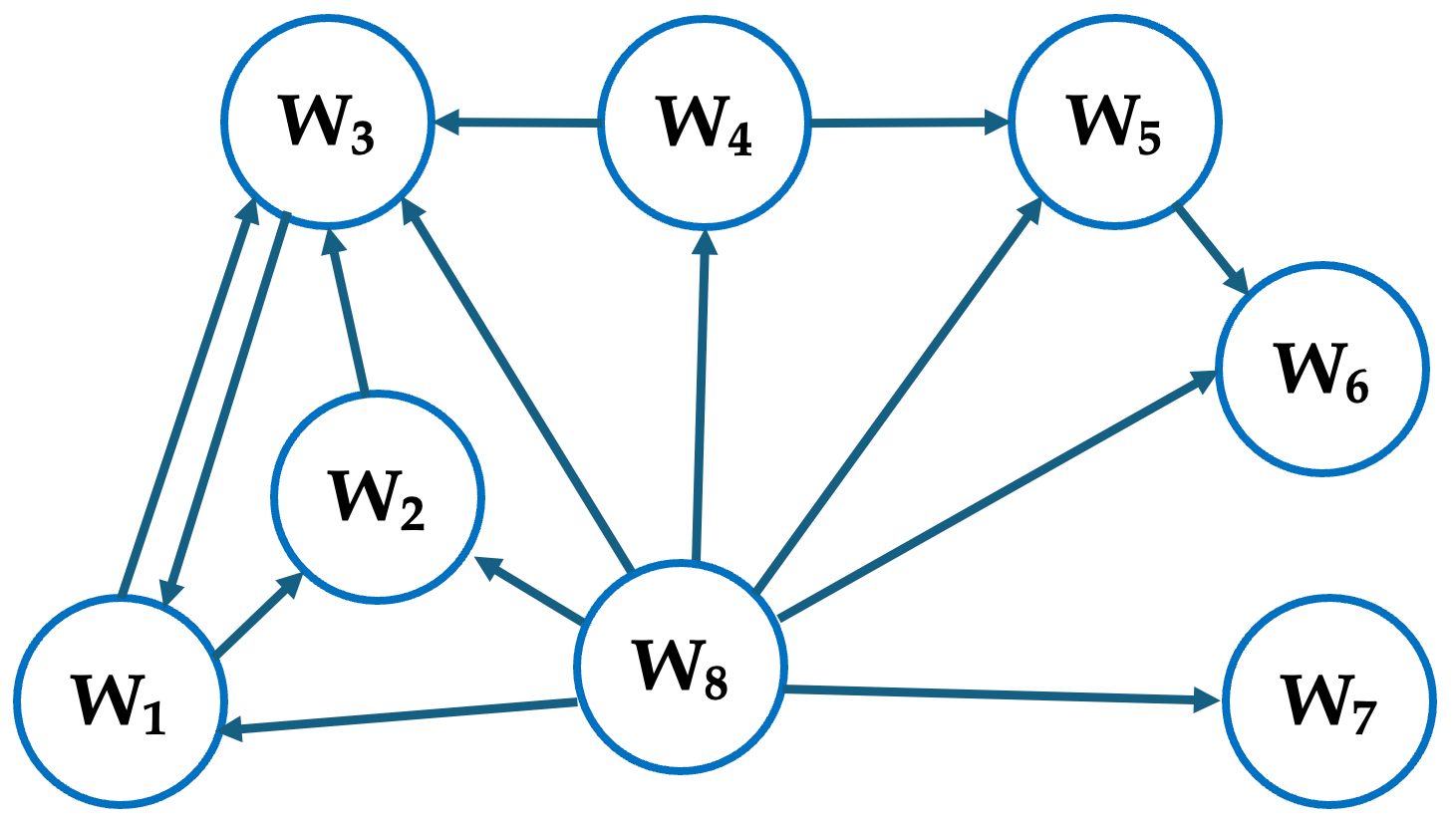
以下，具体例で説明する．図5.2で示すようなウェブ全体のトイモデル（おもちゃのようなモデル）を考える（[LM2006]の例）．矢印は，例えば，$W_1$ から $W_2$ にリンクが張られていることを意味する．そうすると，$W_2$ からはどのウェブページにもリンクが張られていない（例えば，PDFファイルなどが想定される）．グラフ理論ではこのような node を dangling node と呼ぶ．

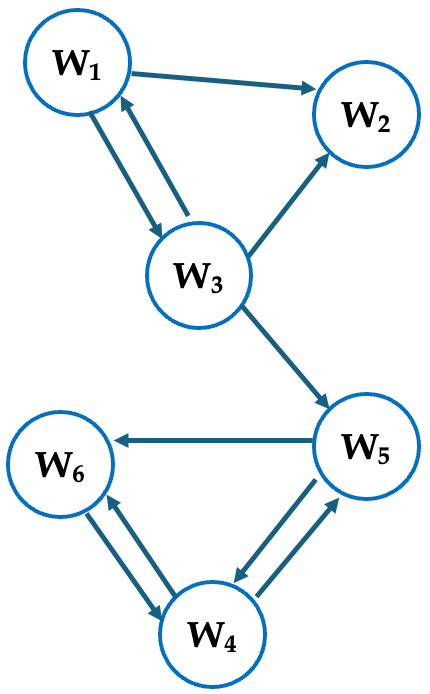
$W_1$ からは $W_2$ と $W_3$ にリンクが張られている．ここで，個別のことは考慮せずに，これらの「寄与」は等価であるとする．すなわち，$W_1$ の持っている重要度 $p_1$ の $\frac12$ ずつが $W_2$ と $W_3$ の重要度 $p_2$ と $p_3$ に寄与すると考える．これが(5.3)の意味である（この場合，$p_2$ と $p_3$ が，それぞれ，$p_i$ の役割になる．一方で，$1\in B_2$ かつ $1\in B_3$ である）．図5.3を見よ．

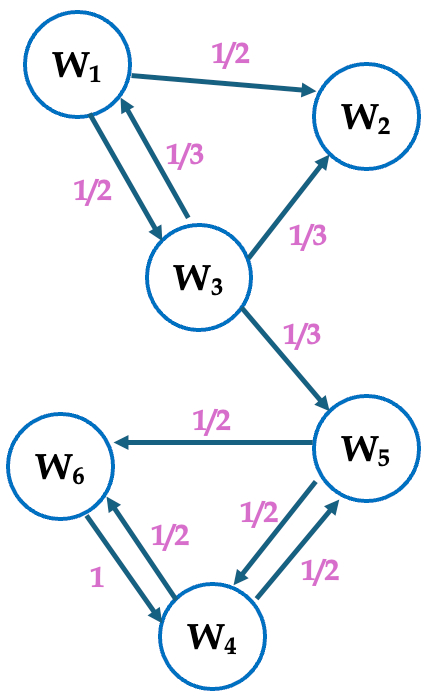
実際，$|W_1|=|W_4|=|W_5|=2$，$|W_2|=0$，$|W_3|=3$，$|W_6|=1$ に注意して，トイモデルに対して(5.3)の関係を書き下してみると，次のようになる： \begin{align} p_1 & = \frac{1}{3}p_3\\ p_2 & = \frac{1}{2}p_1+\frac{1}{3}p_3\\ p_3 & = \frac{1}{2}p_1\\ p_4 & = \frac{1}{2}p_5+p_6\\ p_5 & = \frac{1}{3}p_3+\frac{1}{2}p_4\\ p_6 & = \frac{1}{2}p_4+\frac{1}{2}p_5. \end{align} あるいは， \begin{equation} \tag{5.4} \underbrace{\begin{pmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \\ p_5 \\ p_6 \end{pmatrix} }_{=\boldsymbol{p}} = \underbrace{ \begin{pmatrix} 0 & 0 & \frac13 & 0 & 0 & 0\\ \frac12 & 0 & \frac13 & 0 & 0 & 0\\ \frac12 & 0 & 0 & 0 & 0& 0\\ 0 & 0 & 0 & 0 & \frac12 & 1\\ 0 & 0 & \frac13 & \frac12 & 0 & 0\\ 0 & 0 & 0 & \frac12 & \frac12 & 0 \end{pmatrix} }_{=H} \underbrace{\begin{pmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \\ p_5 \\ p_6 \end{pmatrix} }_{=\boldsymbol{p}} \quad \Leftrightarrow \quad \boldsymbol{p}=H\boldsymbol{p}. \end{equation}

したがって，成分が(5.1)と(5.2)を満たすベクトル $\boldsymbol{p}$ で，(5.4)を満たすものを求めれば良い．それに当たり，差し当たって次の疑問が湧く：

(Q1): (5.4)を満たすベクトル $\boldsymbol{p}$ は一意的に存在するか？
(Q2): (5.4)をどうやって解くか？

まず，(Q1)について，$\boldsymbol{p}$ には明らかに定数倍の不定さがある．すなわち，$\boldsymbol{p}$ が解なら，任意の $0\ne c\in\mathbb{R}$ に対して $c\boldsymbol{p}$ も解となる．なお，この性質により，各成分が非負となるように $\boldsymbol{p}$ を求めておけば，適当に定数倍を調整することにより，(5.2)を実現することは簡単である（したがってこの点については，今後，言及しない）．存在については一旦保留する．次に，(Q2)について，(5.4)すなわち $(IーH)\boldsymbol{p}=\boldsymbol{0}$ は，特異行列 $IーH$ を係数行列とする連立一次方程式である（$IーH$ が正則なら，自明な解 $\boldsymbol{p}=\boldsymbol{0}$ しか存在しないので，明らかに不適）．したがって，最小二乗解などをで解を求める必要がある．しかし，(5.4)をそのままで眺めると，これは，$1$ が $H$ の固有値，$\boldsymbol{p}$ が対応する固有ベクトルと解釈できるので，固有値解法が使えそうである．しかも，冪乗法を使えば，固有ベクトルが直接得られる．したがって，次の(C)が肯定的に確かめられれば，(Q1)と(Q2)は一挙に解決できることになる:

(C): $H$ の絶対最大の固有値は $1$ のみである．しかもそれは単純固有値（固有方程式の根として重根ではない）である．したがって，固有ベクトル $\boldsymbol{p}$ は，定数倍の不定さを除けば一意に定まる．しかも，$\boldsymbol{p}$ の各成分は非負になる（そう採れる）．

注意. 冪乗法と逆冪乗法の説明では，絶対最大の（唯一の）固有値の重複度については，何も言及しなかった．それは，$A$ の対角化可能性を仮定していたためである．しかし，PageRankに現れる行列について，対角化可能性までを要請するのは難しい．

しかし，残念ながら，$H$ について(C)が成り立つことは保証されない．そこで，$H$ を少しずつ修正し，(C)が保証されるようにする．まず，$H$ の第2列目の成分がすべて零であることは都合が悪い．これは，$W_2$ が dangling node であることに起因している． \begin{equation} \boldsymbol{1}_n= \begin{pmatrix} 1 \\ 1 \\ \vdots \\ \vdots \\ 1 \\ 1 \end{pmatrix} \in\mathbb{R}^n ,\qquad \boldsymbol{a}= \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} \in\mathbb{R}^6 \end{equation} とおく．すなわち， $\boldsymbol{1}_n$ はすべての成分が $1$ のベクトル， $\boldsymbol{a}$ は dangling node に対応する成分のみ $1$ とし，その他は $0$ であるようなベクトルである．そして， \begin{equation} \tag{5.5} S=H+\frac{1}{6}\boldsymbol{1}_6\boldsymbol{a}^{\scriptsize \mbox{T}} = H + \begin{pmatrix} 0 & \frac16 & 0 & 0 & 0 & 0\\ 0 & \frac16 & 0 & 0 & 0 & 0\\ 0 & \frac16 & 0 & 0 & 0& 0\\ 0 & \frac16 & 0 & 0 & 0 & 0\\ 0 & \frac16 & 0 & 0 & 0 & 0\\ 0 & \frac16 & 0 & 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & \frac16 & \frac13 & 0 & 0 & 0\\ \frac12 & \frac16 & \frac13 & 0 & 0 & 0\\ \frac12 & \frac16 & 0 & 0 & 0& 0\\ 0 & \frac16 & 0 & 0 & \frac12 & 1\\ 0 & \frac16 & \frac13 & \frac12 & 0 & 0\\ 0 & \frac16 & 0 & \frac12 & \frac12 & 0 \end{pmatrix} \end{equation} とおき，(5.4)の代わりに， \begin{equation} \boldsymbol{p}=S\boldsymbol{p} \end{equation} を考える．この $H$ から $S$ への修正は，どこにもリンクが張られていないウェブページは，全ウェブに平等に寄与があると考えていることに対応している．しかし，これでもまだ，(C)を保証することは難しい．もうひと工夫必要である．

つぎに，私達がウェブを閲覧する際には，目的を持ってリンクを辿っていくこともあるが，往々にして，無目的に適当に（ダラダラと）リンクを辿ることもある（こちらのほうが多い？）．なお，かつてはこの後者の状況を「ネットサーフィン」と表現していたが，この言葉はかなり前に廃れてしまったようである．それはともかく，ランダムなネットサーフィンの効果を入れるために，パラメータ $0< \alpha < 1$ を導入して， \begin{equation} \tag{5.6} G =\alpha S + (1-\alpha) \frac{1}{6} \boldsymbol{1}_6\boldsymbol{1}^{\scriptsize \mbox{T}}_6 \end{equation} とおく．この $G$ をグーグル行列（Google matrix）と言う．行列 $\boldsymbol{1}_6\boldsymbol{1}^{\scriptsize \mbox{T}}_6$ はすべての成分が $1$ の行列なので，$G$ の各成分もすべて正になることに注意せよ．そして，あらためて，(5.4)の代わりに， \begin{equation} \tag{5.7} \boldsymbol{p}=G\boldsymbol{p} \end{equation} を考えるのである．グーグル行列 $G$ に対して，(5.7)を満たすベクトル $\boldsymbol{p}$ で成分が(5.1)と(5.2)を満たすものをGoogleのPageRankベクトルと呼ぶ．

実はこの $G$ は(C)を満たす．それを説明するために，まずは，次の一般的な事実を確認しよう．

$A\in\mathbb{R}^{n\times n}$ の各成分が非負であり，かつ，$A\boldsymbol{1}_n=\boldsymbol{1}_n$ （すなわち，各行の成分和がすべて $1$）を満たすならば，$A$ を確率行列（右確率行列）と言う．$1$ は確率行列 $A$ の固有値であり，対応する固有ベクトルは $\boldsymbol{1}_n$ である．一方で，定理5.2より，$\rho(A)\le 1$なので，これらを合わせると，$\rho(A)=1$ であることがわかる．すなわち，$1$ は確率行列の固有値のうち絶対値が最大になるものである．

正方行列とその転置行列の固有値はすべて一致するので，確率行列 $A$ の転置行列 $A^{\scriptsize \mbox{T}}$ についても，$1$ は絶対値が最大になる固有値であることがわかる．しかし，その（代数的）重複度については何も情報がない．また，絶対値が最大になる固有値が $1$ のみであるかどうかもわからない．

そこで，Perron-Frobeniusの定理を利用する．この定理を述べる前に，少し長くなってしまうが，有向グラフの強連結性と行列の既約性の定義を復習しておく．確率行列とは限らない一般の $A = (a_{ij})\in\mathbb{R}^{n\times n}$（$A = (a_{ij})\in\mathbb{C}^{n\times n}$ でも良い）と，平面上の異なる $n$ 個の点 $\mathrm{P}_1, \mathrm{P}_2, \ldots, \mathrm{P}_n$ を考える．これらの点をノード（node）と呼ぶ． $a_{ij}\ne 0$ のとき，ノード $\mathrm{P}_i$ からノード $\mathrm{P}_j$ へ向かう有向辺 $\overrightarrow{\mathrm{P}_i\mathrm{P}_j}$ を引く（図5.4を見よ）．このようにして，行列 $A$ に対し，それに対応する有向辺の集合 $\mathcal{G}(A)$ を構成できる．これを（有限の）有向グラフと呼ぶ．

図5.4：$\mathrm{P}_i$ から $\mathrm{P}_j$ へ向かう有向辺

例えば， \begin{equation} A_1=\begin{pmatrix} 0&0&1&1\\ 0&0&1&1\\ 1&1&0&0\\ 1&1&0&0 \end{pmatrix},\qquad A_2=\begin{pmatrix} 1&1\\ 0&3 \end{pmatrix} \end{equation} に対しては，$\mathcal{G}(A_1)$ と $\mathcal{G}(A_2)$ は図5.5の通りである．

図5.5：左が $\mathcal{G}(A_1)$，右が $\mathcal{G}(A_2)$

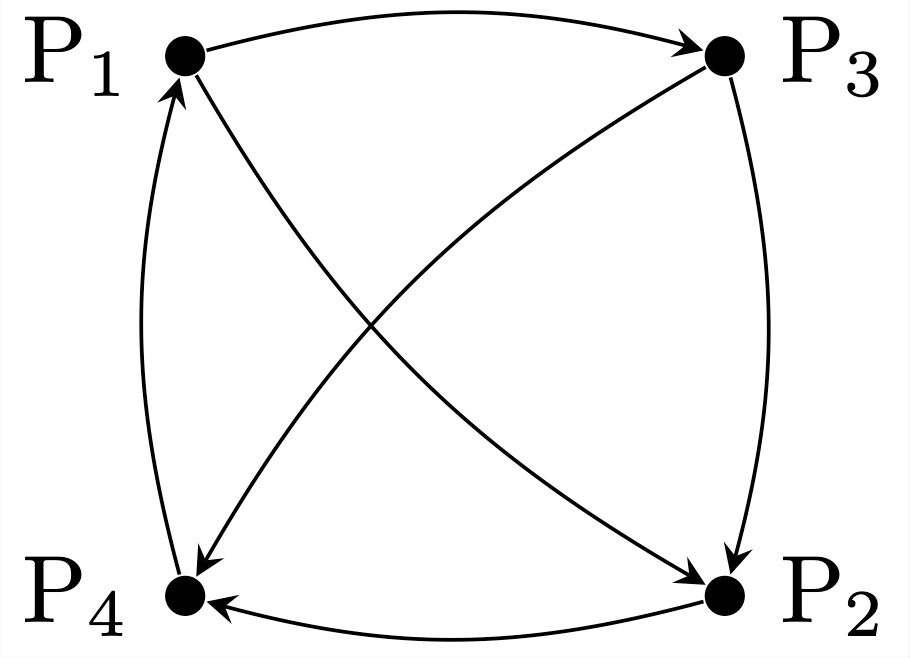
有向グラフが強連結（strongly connected）であるとは，任意のノードの順序対 $(\mathrm{P}_i, \mathrm{P}_j)$ に対して，隣接する有向辺からなる有向パス \begin{equation} \overrightarrow{\mathrm{P}_{l_0}\mathrm{P}_{l_1}},\quad \overrightarrow{\mathrm{P}_{l_1}\mathrm{P}_{l_2}},\quad \cdots,\quad \overrightarrow{\mathrm{P}_{l_{r-1}}\mathrm{P}_{l_r}},\quad (l_0=i,\ l_r=j) \end{equation} が存在し，$\mathrm{P}_i$ から $\mathrm{P}_j$ へ到達できることをいう（このとき，このパスの長さは $r$ であると言う）．上の $\mathcal{G}(A_1)$ は強連結，$\mathcal{G}(A_2)$ は強連結ではない．実際，$\mathcal{G}(A_2)$ は $\mathrm{P}_{2}$ から $\mathrm{P}_{1}$ へ到達するパスが存在しない．そして，行列 $A$ に対して，対応する有向グラフ $\mathcal{G}(A)$ が強連結のとき，$A$ は既約行列 (irreducible matrix)であると言う．上の $A_1$ は既約行列，$A_2$ は既約行列ではない（それを可約行列と言う）．

定理 5.4. (Perron-Frobenius) $A\in\mathbb{R}^{n\times n}$ は各成分が非負でありかつ既約行列であるとする．このとき，$\rho(A)$ は $A$の単純固有値であり，対応する固有ベクトルで各成分が正であるようななものが存在する．$\blacksquare$

この定理については，例えば，[Varga2000]のTheorem 2.7を見よ．これより，確率行列 $A$ の転置行列 $A^{\scriptsize \mbox{T}}$ が，さらに既約行列ならば， $1$ は単純固有値であり，しかも対応する固有ベクトルで各成分が正なものが存在することがわかるのである．しかし，この定理では， $\rho(A)=|\lambda|$ を満たす（$\rho(A)$ 以外の）固有値 $\lambda\in\mathbb{C}$ の存在は排除できていない．そこで，次を使う．

定理 5.5. $A\in\mathbb{R}^{n\times n}$ の各成分が正ならば（このとき，対応する有向グラフは強連結であり，したがって，各成分が非負な既約行列となるのでPerron-Frobeniusの定理を適用できるが）， $\rho(A)=|\lambda|$ を満たす $A$ の固有値 $\lambda\in\mathbb{C}$ は，$\lambda=\rho(A)$ のみである． $\blacksquare$

この定理は，例えば，[Varga2000]のLemma 2.15（とDefinition 2.10）を見よ．

さて，これでやっと準備が整った．(5.5)で定義された行列 $S$ と(5.6)で定義された行列 $G$ の考察に戻ろう．各々の転置行列 $S^{\scriptsize \mbox{T}}$ と $G^{\scriptsize \mbox{T}}$ は確率行列である（そうなるように構成した！）．したがって，$1$ は，その転置行列 $S$ と $G$ の絶対値最大の固有値である．次に， $G$ の各成分は正なので，対応する有向グラフは強連結であり，したがって，$G$ は各成分が非負であり既約行列となる．結果的に，Perron-Frobeniusの定理と定理5.5が適用できる．すなわち，$\lambda_1,\ldots,\lambda_6$ を $G$ の固有値とすると， \begin{equation*} |\lambda_1|\le\cdots \le |\lambda_5| < \lambda_6=\rho(G)=1, \end{equation*} かつ，$1$ は単純固有値で対応する固有ベクトルは（定数倍を調整すれば）各成分が正となる．これで，$G$ が(C)の性質を持つことが確かめられた．したがって，あらためて，$\boldsymbol{p}^{(0)}$ を適当に選んだ上で，冪乗法を使って， \[ \boldsymbol{q}^{(k)}=G\boldsymbol{p}^{(k)},\quad \boldsymbol{p}^{(k+1)}=\frac{1}{\|\boldsymbol{q}^{(k)}\|}\boldsymbol{q}^{(k)}\qquad (k=0,1,\ldots) \] とすれば，十分大きい $m$ に対して，$\boldsymbol{p}^{(m)}$ が (5.7)の解 $\boldsymbol{p}$ の十分良い近似値を与えることが期待されるし，実際，その期待が正しいことが数学的に保証されているのである．なお，$\boldsymbol{p}^{(0)}$ としては，各成分が正になるようなベクトルを採っておけば，$\boldsymbol{p}^{(k)}$ の各成分も自然に正となる．

しかしながら，$S$ は既約行列でないので（実際，到達できないノードの順序対がいくらでもある），このようなことは言えない．$H$については，そもそも，その転置が確率行列ではない．

それでは，実際に，図5.2のウェブのトイモデルに対して各ウェブページの重要度を計算してみよう．そのためには，In [3]:で作った power1(A, initial, tolerance)がそのまま使える．Google行列 $G$ を定義するために，次を確認しておこう．

In [19]:
n = 4
A = np.ones((n,n))
avec = np.zeros(n)
avec[1] = 1
B = np.outer(np.ones(n), avec)
C = A + (1/n)*B
print(f"A={A}")
print(f"a={avec}")
print(f"B={B}")
print(f"C={C}")
  
Out [19]:
A=[[1. 1. 1. 1.]
 [1. 1. 1. 1.]
 [1. 1. 1. 1.]
 [1. 1. 1. 1.]]
a=[0. 1. 0. 0.]
B=[[0. 1. 0. 0.]
 [0. 1. 0. 0.]
 [0. 1. 0. 0.]
 [0. 1. 0. 0.]]
C=[[1.   1.25 1.   1.  ]
 [1.   1.25 1.   1.  ]
 [1.   1.25 1.   1.  ]
 [1.   1.25 1.   1.  ]]

そして，あらためて，$G$ を定義して，冪乗法を実行する．

In [20]:
n = 6 #全ウェブ数
H = np.array([
    [0,0,1/3,0,0,0],
    [1/2,0,1/3,0,0,0],
    [1/2,0,0,0,0,0],
    [0,0,0,0,1/2,1],
    [0,0,1/3,1/2,0,0],
    [0,0,0,1/2,1/2,0]
    ]) 
avec = np.zeros(n)
avec[1] = 1
S = H + (1/n)*np.outer(np.ones(n), avec)
print(f"H={H}")
print(f"a={avec}")
print(f"S={S}")
  
Out [20]: 
H=[[0.         0.         0.33333333 0.         0.         0.        ]
 [0.5        0.         0.33333333 0.         0.         0.        ]
 [0.5        0.         0.         0.         0.         0.        ]
 [0.         0.         0.         0.         0.5        1.        ]
 [0.         0.         0.33333333 0.5        0.         0.        ]
 [0.         0.         0.         0.5        0.5        0.        ]]
a=[0. 1. 0. 0. 0. 0.]
S=[[0.         0.16666667 0.33333333 0.         0.         0.        ]
 [0.5        0.16666667 0.33333333 0.         0.         0.        ]
 [0.5        0.16666667 0.         0.         0.         0.        ]
 [0.         0.16666667 0.         0.         0.5        1.        ]
 [0.         0.16666667 0.33333333 0.5        0.         0.        ]
 [0.         0.16666667 0.         0.5        0.5        0.        ]]

まず，$\alpha=0.9$とする．最終的には，(5.2)を満たすように定数倍したベクトルも表示する．

In [21]:
alpha = 0.9
G = alpha*S + (1/n)*(1-alpha)*np.ones_like(S) # Google行列

tol = 1e-6  # 許容誤差
init = np.random.rand(6)# 初期ベクトル
iteration, eval, increment, evec = power1(G, init, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])

# PageRankベクトル
final = np.copy(evec[-1,:])
final = (1/np.sum(final))*final
print("PageRankベクトル",final)

Out [21]: 
反復, 固有値, 増分, 固有ベクトル
0, 0.8946, 1.000e+00,  [0.32955789 0.46013785 0.27723009 0.34188605 0.25006884 0.65068252]
1, 0.9241, 3.185e-02,  [0.17983353 0.31969698 0.24125986 0.75982063 0.32492902 0.35262042]
2, 1.0430, 1.140e-01,  [0.15785791 0.23941472 0.16647176 0.55211017 0.5024463  0.57686281]
....
22, 1.0000, 1.476e-06,  [0.07147573 0.10364071 0.07972309 0.72040697 0.39565719 0.54978473]
23, 1.0000, 1.055e-06,  [0.07147432 0.10363832 0.07972145 0.72040771 0.39565662 0.54978503]
24, 1.0000, 5.714e-07,  [0.07147347 0.10363686 0.07972046 0.72040805 0.39565644 0.54978525]
PageRankベクトル [0.03721257 0.05395841 0.04150636 0.37507958 0.20599805 0.28624503]

これより，$p_4>p_6>p_5>p_2>p_3>p_1$ であり，各ウェブは重要度の高い順に $W_4,W_6,W_5,W_2,W_3,W_1$ と並べられる．

次に，$\alpha=0.6$とする．

In [22]:
alpha = 0.6
G = alpha*S + (1/n)*(1-alpha)*np.ones_like(S) # Google行列

tol = 1e-6  # 許容誤差
init = np.random.rand(6)# 初期ベクトル
iteration, eval, increment, evec = power1(G, init, tol)

print("反復, 固有値, 増分, 固有ベクトル")
for i in range(iteration):
  print(f"{i:d}, {eval[i]:.4f}, {increment[i]:.3e}, ",evec[i,:])

# PageRankベクトル
final = np.copy(evec[-1,:])
final = (1/np.sum(final))*final
print("PageRankベクトル",final)
  
Out [22]: 
反復, 固有値, 増分, 固有ベクトル
0, 0.5397, 1.000e+00,  [0.26995191 0.08081536 0.6774701  0.18186965 0.11561428 0.64434919]
1, 0.9194, 4.130e-01,  [0.32263373 0.41767697 0.25866358 0.6580433  0.38666543 0.26835691]
2, 1.0088, 8.862e-02,  [0.25450583 0.3539809  0.30081312 0.48603617 0.45739505 0.52344472]
....
12, 1.0000, 1.223e-06,  [0.23630586 0.30719879 0.25599825 0.60589655 0.41807702 0.49229496]
13, 1.0000, 2.180e-06,  [0.23630369 0.30719526 0.25599574 0.60590317 0.41807219 0.49229545]
14, 1.0000, 2.989e-09,  [0.23630295 0.30719403 0.2559949  0.60590259 0.41807384 0.49229632]
PageRankベクトル [0.10204101 0.13265339 0.11054444 0.26164256 0.18053382 0.21258478]

この場合も，各ウェブは重要度の高い順に $W_4,W_6,W_5,W_2,W_3,W_1$ と並べられる．

注意. ここで計算例は示さないが，この場合は，（数学的な保証はないが）上の$H$ や $S$ をそのまま使っても，計算は可能である．特に，$S$ について固有値 $1$ に対する固有ベクトルの各成分は非負になることがわかっている（[室田・杉原2013]の定理2.2など）．

注意. 成り行き上，図5.2のウェブのトイモデルに対して説明したが，一般の場合も同様に考えれば良い．すなわち，$N$ 個のウェブページ $W_1,\ldots,W_N$ について，そのリンクの関係を表現した行列 $H\in\mathbb{R}^{n\times n}$ とdangling node に対応する成分のみ $1$，その他は $0$ であるようなベクトル $\boldsymbol{a}$ を作った後に， \begin{align*} S&=H+\frac{1}{n}\boldsymbol{1}_n\boldsymbol{a}^{\scriptsize \mbox{T}},\\ G&=\alpha S+(1-\alpha) \frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}^{\scriptsize \mbox{T}}_n \end{align*} とすれば良い．

注意. 行列の既約性には同値な定義が複数ある．興味のある人は，[齊藤2012]を見よ．

問題

上記の入力と出力をすべて確かめよ．
行列やパラメータ値を変えて，計算を再試行せよ．
例題を自分で設定して，上記の方法を試せ．

課題

課題5.1

2つの行列 \[ A_+= \begin{pmatrix} 30 & 2 & 3 & 13 \\ 5 & 11 & 10 & 8\\ 9 & 7 & 6 &12 \\ 4 & 14 & 15 & 1 \end{pmatrix} ,\quad A_-= \begin{pmatrix} -30 & 2 & 3 & 13 \\ 5 & 11 & 10 & 8\\ 9 & 7 & 6 &12 \\ 4 & 14 & 15 & 1 \end{pmatrix} \] を考える第 $(1,1)$ 成分以外の成分は全て等しいことに注意せよ．$A_{+}$ の絶対値最大の固有値と固有ベクトルを冪乗法を使って求めよ．次に，$A_{-}$ の絶対値最大の固有値と固有ベクトルを冪乗法を使って求め，$A_{+}$ の場合との収束の速さの違いについて考察せよ．

課題5.2

行列 \[ A= \begin{pmatrix} 0 & 0 & 0 & -26 \\ 1 & 0 & 0 & 51\\ 0 & 1 & 0 &-33 \\ 0 & 0 & 1 & 9 \end{pmatrix} \] の絶対値最小の固有値を逆冪乗法で求めよ．また，絶対値最大の固有値を求めるために冪乗法を適用すると，どのような結果になるかを報告せよ．

課題5.3

図5.6に示すウェブのモデルに対して，各ウェブページの重要度をPageRankにより計算せよ．特に，$\alpha$ 変化させたときの重要度の順位付けの変化について調べよ．

参考文献

[BP1998] S. Brin and L. Page, The Anatomy of a Large-Scale Hypertextual Web Search Engine, Computer Networks and ISDN Systems, Vol. 30, Issues 1–7, 107–117, 1998
[LM2006] A. N. Langville and C. D. Meyer, Google’s PageRank and Beyond: The Science of Search Engine Rankings, Princeton University Press, 2006.
[室田・杉原2013] 室田一雄，杉原正顯，線形代数II，東京大学工学教程，丸善出版，2013年
[PBMW1999] L. Page, S. Brin, R. Motwani, T. Winograd, PageRank Citation Ranking: Bringing Order to the Web, Technical Report. Stanford InfoLab., 1999
[QSG2014] A. Quarteroni, F. Saleri, P. Gervasio, Scientific Computing with MATLAB and Octave (4th edition), Springer, 2014（加古孝，千葉文浩訳，MATLABとOctaveによる科学技術計算，丸善出版，2014年）
[齊藤2012] 齊藤宣一，数値解析入門，東京大学出版会，2012年
[Varga2000] R. S. Varga, Matrix Iterative Analysis (Springer Series in Computational Mathematics 27) , Springer, 2000.

PageRank以外の固有値問題の具体的な応用例については[QSG2014]の6.1節を見よ．画像圧縮や都市間の鉄道ネットワークへの応用例が述べられている．

付録：QR分解とQR法

以下は，講義中には説明しません．

$A\in\mathbb{R}^{n\times n}$ を，直交行列 $Q$ と上三角行列 $R$ を用いて， \begin{equation*} A=QR ,\quad Q^{\scriptsize\mbox{T}}Q=QQ^{\scriptsize\mbox{T}}=I, \quad R= \begin{pmatrix} r_{1,1} & \cdots & r_{1,n}\\ % & r_{2,2} & & \vdots \\ & \ddots & \vdots \\ {\Large 0} & & r_{n,n}\\ \end{pmatrix} \end{equation*} の形に書くことを，QR分解と呼ぶ．このような分解が得られていれば，連立一次方程式 $A\boldsymbol{x}=\boldsymbol{b}$ は， \begin{equation*} QR\boldsymbol{x}=\boldsymbol{b} \quad \Leftrightarrow \quad \begin{cases} R\boldsymbol{x}=\boldsymbol{c} &\\ Q\boldsymbol{c}=\boldsymbol{b} & \end{cases} \end{equation*} と同値であるから，はじめに $\boldsymbol{c}=Q^{-1}\boldsymbol{b}=Q^{\scriptsize\mbox{T}} \boldsymbol{b}$ で $\boldsymbol{c}$ を求めておいて，後は $R\boldsymbol{x}=\boldsymbol{c}$ にしたがって， $\boldsymbol{x}$ を計算することができる．

任意の正則行列$A\in\mathbb{R}^{n\times n}$は，グラム・シュミットの直交化法によりQR分解が可能である．QR分解の一意性を述べるために， \begin{equation} S= \begin{pmatrix} s_{1} & & {\Large 0}\\ & \ddots & \\ {\Large 0} & & s_{n}\\ \end{pmatrix}\in\mathbb{R}^{n\times n},\qquad s_i^2=1\quad (i=1,\ldots,n) \label{eq:l.6.55} \end{equation} を満たす対角行列を考える．このような形の行列を，符号行列と呼ぶ．正則行列$A\in\mathbb{R}^{n\times n}$ が，$A=Q_1R_1$，$A=Q_2R_2$ と二通りにQR分解できたとすると，$Q_1=SQ_2$，$R_1=R_2S$ を満たす符号行列 $S\in\mathbb{R}^{n\times n}$ が存在する．

詳しくは，[齊藤2012]の2.7節を見よ．

$A\in\mathbb{R}^{n\times n}$のすべての固有値を，反復的にかつ同時的に計算する方法であるQR法について述べる．そのために，$A$ が，相異なる $n$ 個の実固有値 $\lambda_1,\ldots,\lambda_n$ を持つと仮定する．このとき，$A$ は適当な直交行列 $U$ により，\begin{equation} U^{\scriptsize\mbox{T}} AU= \begin{pmatrix} b_{1,1} & \cdots & b_{1,n}\\ % & b_{2,2} & & \vdots \\ & \ddots & \vdots \\ {\Large 0} & & b_{n,n}\\ \end{pmatrix} =B ,\qquad b_{i,i}=\lambda_i\quad (1\le i\le n) \label{eq:e.3.0} \end{equation} と表現できる．これは，Schur分解の実行列版である．例えば，[齊藤2012]の命題2.8.1と注意2.8.4を見よ．

したがって，このような $U$ を求めることができれば，すべての固有値が同時に求まることになるが，もちろんそれは難しい．そこで，$U$ に十分近い行列 $\tilde{Q}$ を作って，$\tilde{Q}^{\scriptsize\mbox{T}} A\tilde{Q}$ を計算すれば，この対角成分が求めたい $A$ の固有値の近似値であろうことが期待できる．もう少し具体的には，「何らかの基準」で直交行列の列 $\{Q_1,Q_2,\ldots,\}$ を作って，$A_1=A$， \begin{equation} A_{k+1}=Q_k^{\scriptsize\mbox{T}} A_{k}Q_k= Q_k^{\scriptsize\mbox{T}} Q_{k-1}^{\scriptsize\mbox{T}} \cdots Q_1^{\scriptsize\mbox{T}} A \underbrace{Q_1 \cdots Q_{k-1}Q_k}_{=\tilde{Q}_k}=\tilde{Q}_k^{\scriptsize\mbox{T}} A\tilde{Q}_k \end{equation} とする．明らかに，$\tilde{Q}_k$ は直交行列である．「何らかの基準」は，当然，$k\to\infty$　の際， $\tilde{Q}_k\to U$，$A_k\to B$ となるように設定しなければならない．そして，十分大きな $k$ をとり，$A_k$ の対角成分を$\lambda_1,\ldots,\lambda_n$ の近似値として採用するわけである．

QR法は，その名前から想像できるように，QR分解を応用して直交行列の列 $\{Q_1,Q_2,\ldots,\}$ を生成する．具体的には，

$A_1=A$とする．
$k=1,2,\ldots$ に対して，$A_k$ を $A_k=Q_kR_k$（$Q_k$ は直交行列， $R_k$ は上三角行列）とQR分解し， \begin{equation*} A_{k+1}=R_kQ_k \end{equation*} と更新する．

このように，QR法の算法は極めて単純である．しかも， $R_k=Q_k^{-1}A_{k}=Q_k^{\scriptsize\mbox{T}} A_k$ なので，$A_{k+1}=Q_k^{\scriptsize\mbox{T}} A_kQ_k$ と書ける．さらに， \begin{equation} A^k=\tilde{Q}_k\tilde{R}_k,\quad \tilde{Q}_k=Q_1 \cdots Q_k,\quad \tilde{R}_k=R_k\cdots R_1 \quad (k\ge 1) \end{equation} が成り立つ．

QR法の収束については，例えば，[齊藤2012]の5.3節を見よ．

実際にQR法を実行してみよう．本来ならば，（教育的な配慮からは） QR分解の部分も自作するのが望ましいが，今回は， numpyの linalgの関数を利用する．

In [23]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
Q,R = la.qr(A)
print("Q=\n",Q)
print("Q*Q.T=\n",Q@Q.T)
print("R=\n",R) 
  
Out [23]:
=
 [[-0.76249285  0.62855011  0.14391842 -0.05307449]
 [-0.60999428 -0.77741724  0.14391842 -0.05307449]
 [-0.15249857 -0.01654079 -0.89229418 -0.42459591]
 [-0.15249857 -0.01654079 -0.40297156  0.90226632]]
Q*Q.T=
 [[ 1.00000000e+00 -4.25533324e-17  5.10976254e-17 -1.62255567e-17]
 [-4.25533324e-17  1.00000000e+00  3.84593793e-17 -1.53901357e-17]
 [ 5.10976254e-17  3.84593793e-17  1.00000000e+00 -1.17695776e-16]
 [-1.62255567e-17 -1.53901357e-17 -1.17695776e-16  1.00000000e+00]]
R=
 [[-6.55743852 -6.40493995 -2.28747855 -2.28747855]
 [ 0.         -1.40596735 -0.24811189 -0.24811189]
 [ 0.          0.         -4.087283   -3.10863778]
 [ 0.          0.          0.          2.65372446]]

これを用いれば，QR法の計算は次のように実行できる．

In [24]:
def qr_method(A, tol):
  kmax = 100
  Ak = np.copy(A)
  eval = np.diag(Ak)

  for k in range(kmax):
    Q, R = la.qr(Ak)  
    Ak = R@Q
    eval = np.vstack((eval, np.diag(Ak)))
    if np.abs(np.diag(Ak) - np.diag(A)).max() < tol:
      break
    A = np.copy(Ak)
  
  return k, eval

In [25]:
A=np.array([[5,4,1,1], [4,5,1,1],[1,1,4,2],[1,1,2,4]])
tol=1e-9

iteration, eval = qr_method(A, tol)
print("反復, 固有値")
for i in range(iteration):
  print(f"{i:d}, ",eval[i,:])
  
Out [25]: 
反復, 固有値
0,  [5. 5. 4. 4.]
1,  [9.60465116 1.10123119 4.89975145 2.3943662 ]
2,  [9.92197883 1.00109809 5.01422715 2.06269592]
3,  [9.98053357 1.00001118 5.00955502 2.00990023]
4,  [9.99512184 1.00000011 5.00330192 2.00157613]
5,  [9.99877959 1.         5.0009686  2.0002518 ]
6,  [9.99969484 1.         5.00026489 2.00004027]
7,  [9.99992371 1.         5.00006985 2.00000644]
8,  [9.99998093 1.         5.00001804 2.00000103]
9,  [9.99999523 1.         5.0000046  2.00000016]
10,  [9.99999881 1.         5.00000117 2.00000003]
11,  [9.9999997  1.         5.00000029 2.        ]
12,  [9.99999993 1.         5.00000007 2.        ]
13,  [9.99999998 1.         5.00000002 2.        ]
14,  [10.  1.  5.  2.]

---「5. 固有値問題」はこれで終了---